Evaluation Metric¶
In supervised machine learning, one typically has labeled training data. For example, this dataset identifies whether people are aliens.
| age | weight | name | is_alien |
|-----|--------|---------|----------|
| 135 | 91 | Zeltron | TRUE |
| 71 | 120 | Susan | FALSE |
| 16 | 120 | Kyle | TRUE |
| 35 | 204 | Ryan | FALSE |
| 64 | 144 | Martha | FALSE |
| 241 | 150 | Bobby | TRUE |
| 205 | 33 | Kal-El | TRUE |We might use this data to train two models, A and B, which can be used to predict whether someone is an alien.
Given a new (or potentially the same) labeled dataset,
|---- model inputs -----| |- truths -|
| age | weight | name | | is_alien |
|-----|--------|--------| |----------|
| 27 | 307 | Alice | | FALSE |
| 100 | 188 | Raya | | FALSE |
| 31 | 156 | X'Z-Kl | | TRUE |
| 15 | 143 | Ralf | | FALSE |We can use models A and B to make predictions about each person.
|---- model inputs -----| |----- predicitons -----| |- truths -|
| age | weight | name | | A preds | | B preds | | is_alien |
|-----|--------|--------| |----------| |----------| |----------|
| 27 | 307 | Alice | | TRUE | | FALSE | | FALSE |
| 100 | 188 | Raya | | FALSE | | FALSE | | FALSE |
| 31 | 156 | X'Z-Kl | | TRUE | | FALSE | | TRUE |
| 15 | 143 | Ralf | | FALSE | | TRUE | | FALSE |Which model is better?
The purpose of an evaluation metric is convert a set of predictions and corresponding truths into a numeric score.
Evaluation metrics represent how well a set of predictions match the truth. Given scores for two models A and B, one can claim that A is better than B or vice versa.
In the above example, an obvious choice for an evaluation metric is accuracy rate - a metric that measures the percent of predictions which are correct. Model A's accuracy rate on the validation data was 75% while B's accuracy rate was 50%, thus we conclude that model A is probably better than model B, ignoring additional information.
Subjectivity¶
Evaluation metrics are not subjective. They are definitive. They claim that A is better than B or B is better than A. (This is why we like them.) However, the choice of evaluation metric is subjective and depends largely on the use case.
For example, it may be the case that predicting someone is an alien when they're not (false positive) is no big deal, but predicting someone is not an alien when in fact they are (false negative) is highly problematic. Therefore, we may prefer an evaluation metric that penalizes false negatives more than false positives.
Direction¶
There is no standard direction for evaluation metrics. For example, accuracy rate increases as the quality of predictions improves. However, mean squared error decreases as the quality of predictions improves.
Loss Function¶
Loss functions are just differentiable evaluation metrics. They typically arise in the context of gradient descent.
Typically one's goal is to optimize an evaluation metric. However, the fitting procedure of many machine learning models (boosted trees, neural networks, generalized linear models) uses gradient descent which can only descend on a differentiable function. Lots of evaluation metrics (accuracy rate, area under the ROC curve, mean absolute error) are not differentiable!
When an evaluation metric is not differentiable, but a differentiable scoring function is required for your model's fitting procedure, you must select a loss function that is "close in spirit" to your evaluation metric.
For example, if your evaluation metric is accuracy rate you might use log loss as your loss function to train a neural network or logistic regression model. In general, improvement in log loss corresponds to improvement in accuracy rate.
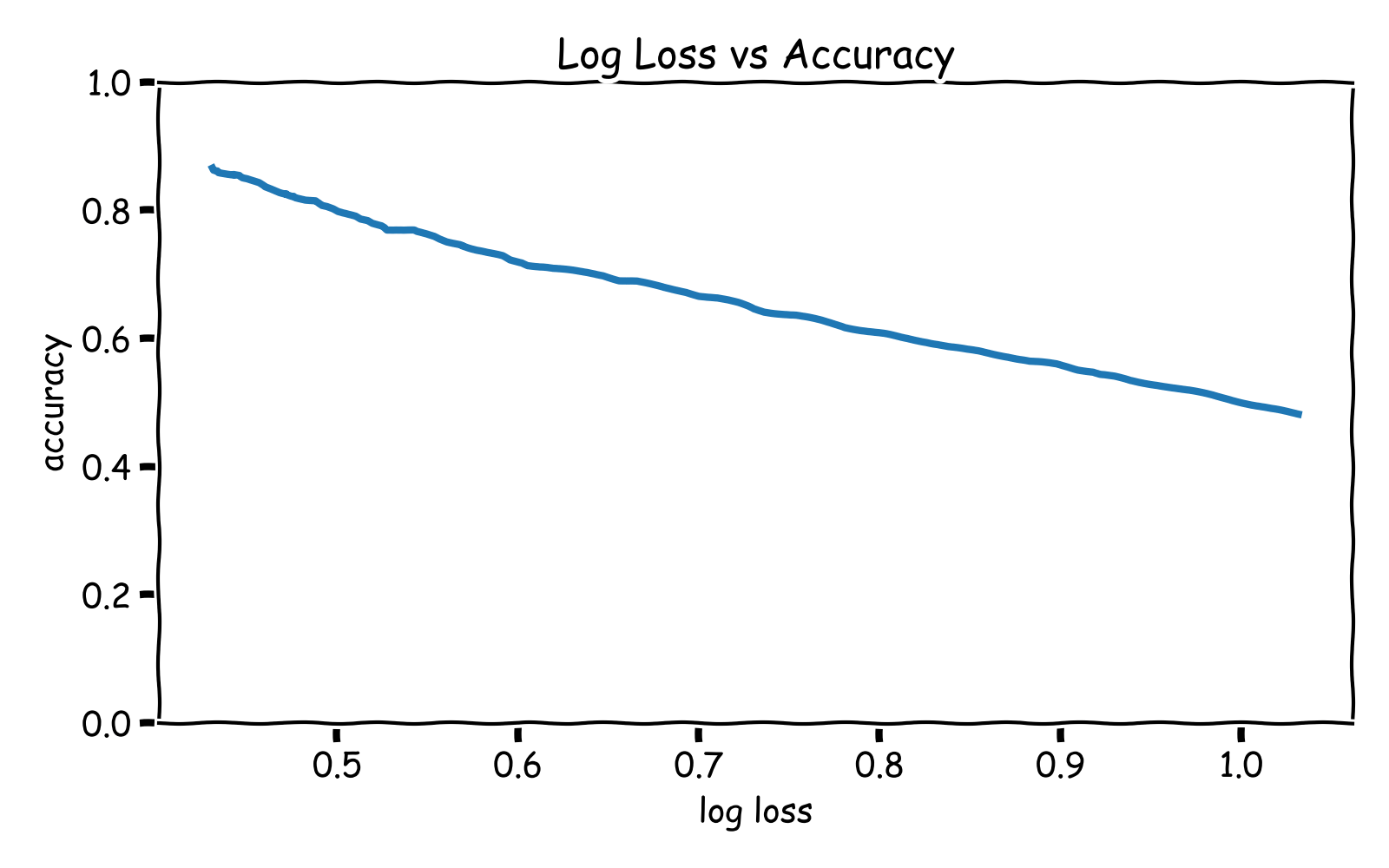
If your evaluation metric is differentiable, it should be used as your model's loss function!